In previous sections I explained the basic roulette computer algorithm which is used by almost every roulette computer. Again, like visual ballistics, they simply determine which number is under the reference diamond when the ball is predicted to fall. Visual ballistics doesn’t usually use “timings” as such, but it doesn’t need to because the time it takes for the ball to do its last 4 revolutions is much the same on any different spin. So with this very simplistic approach, we are ASSUMING the ball will decelerate at the same rate on different spins. Does it actually? . . . NO.
The reality is roulette is a very dynamic game. The physical properties of the wheel and ball gradually change over time. For example, the ball track may gather some dust or grit. The ball may develop a coating of sweat, oil or dust from the dealer’s fingers. The air pressure in the casino will vary over time, thereby affecting the deceleration rate of the ball. This all means that over time, the ball’s deceleration rate can and will change. And if you incorrectly assume the deceleration rate will stay the same, as time progresses, predictions will become less accurate.
Every roulette computer from other vendors I’ve tested makes the same incorrect assumption that the ball deceleration rate will stay the same. Or from a simplistic perspective, that when the ball reaches 1300ms per revolution, that it will always have 7 revolutions remaining. The assumption is wrong, and every simplistic computer assumes it including all of Miro Zirdum’s computers, all of Mark Howe’s computers, and also Michael Barnett’s computer. My most basic computers also make this incorrect assumption. The only roulette computers that adjust for ball deceleration rate changes are my Uber and Hybrid versions.
The effect of ball deceleration rate changes
Let’s assume you begin roulette computer application with a perfect model of the ball’s deceleration rate, and that you can accurately determine how many revolutions remain for the ball once it passes a certain threshold speed. Now you start collecting data, writing down the reference number and winning number (A,B) as explained in previous pages here. After about 2 hours, you will have about 30 spins for each direction.
By now, almost certainly the ball deceleration rate will have changed. There are many effects of this, including but not limited to:
* With the basic “visual ballistics approach”: The ball completes perhaps 1 revolution more or 1 revolution less than it did before. This means your betting area will be roughly 9-12 pockets off target, and instead of your bets targeting the correct area, they avoid it. So you have gone from a strong win, to a strong loss. The end result is you have either no edge at all (random results), or lose even more than you would with random bet selection.
* If you do not account for ball deceleration changes and attempt to determine the range of ball speeds that result in the ball hitting a specific diamond: It is simply not possible because the smallest variations of ball deceleration rate changes completely change which diamond will be hit. Your result can only be accurate in the short term while the ball’s deceleration rate remains consistent. After even a slight change, you lose all accuracy, or even end up avoiding the winning sectors.
Mark Howe’s roulette computers have similar adaptations to the traditional algorithm, with strangely worse results than simpler algorithms. He deceptively claims his latest device adjusts for ball deceleration rate changes, but it does no such thing. Miro Zirdum’s devices also only use the basic algorithm. His only versions that attempt additional functions are the FFA and Acrobat, and these will be discussed later. But none of his devices make any adjustments for ball deceleration rate changes. This alone renders any other potentially effective functions completely ineffective. This is because the slight variations in ball deceleration rate changes make whatever the computer may have learned to become “old news”. It is either a consequence of his hardware (microprocessors) not being capable of handling sufficiently complex algorithms, or he is unaware of what needs to be done.
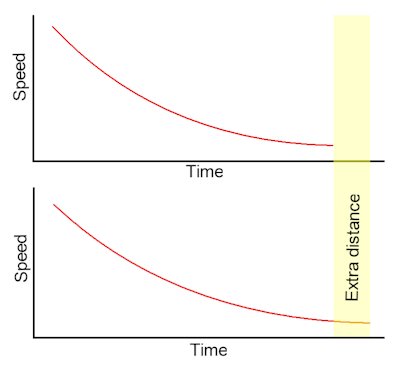
Left is a simplistic visual chart showing how a very slight variation in ball deceleration rates will affect the overall ball travel distance. The difference is completely in perceivable to the naked eye, but in this case is the equivalent of 2 ball revolutions the difference. This is common ball behavior and unless the computer adjusts for the variations properly, full accuracy cannot be achieved. Additionally, the failure eventually leads the player to bet in areas that avoid the correct wheel sector.
